字符串匹配

Trie

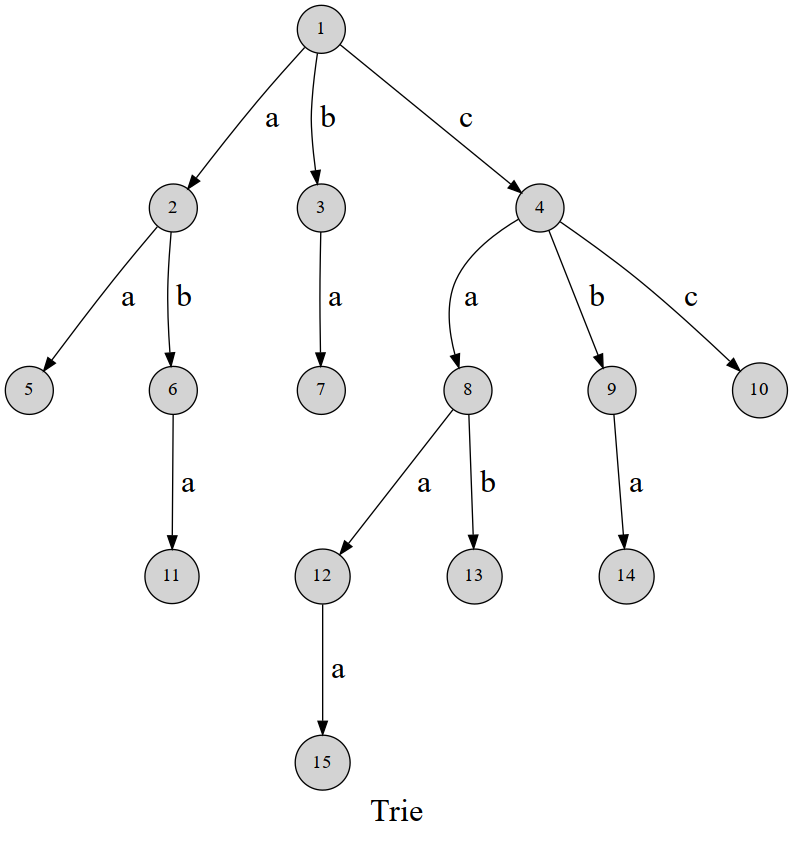
字典树，英文名 trie。

KMP

该算法由 Knuth、Pratt 和 Morris 在 1977 年共同提出。

前缀函数

• 定义：对于一个长度为 n 的字符串，前缀函数/前缀数组p是一个长度为 n 的数组。 其中其中 p[i] 的定义是：子串 s[0 … i] 最长的相等的真前缀与真后缀的长度。
• 举例来说，对于字符串 abcabcd :
  • p[0]=0，p[1]=0，p[2]=0，
  • p[3]=1，因为 abca 只有一对相等的真前缀和真后缀：a，长度为 1
  • p[4]=2，因为 abcab 相等的真前缀和真后缀只有 ab，长度为 2
  • p[6]=0，因为 abcabcd 无相等的真前缀和真后缀
  • 可以计算字符串 aabaaab 的前缀函数为 [0, 1, 0, 1, 2, 2, 3]

简单版实现

vector<int> prefix_function(string s) {
  int n = (int)s.length();
  vector<int> pi(n);
  for (int i = 1; i < n; i++)
    for (int j = i; j >= 0; j--)
      if (s.substr(0, j) == s.substr(i - j + 1, i+1)) {
        pi[i] = j;
        break;
      }
  return pi;
}

时间复杂度为 O(n^3)

优化1

• 我们发现一个重要的规律：相邻的前缀函数值至多增加1
• 只需如此优化：当取一个新的可能更大的 p[i+1] 时，必然要求新增的 s[i+1] 也与之对应的字符匹配，即 s[i+1]=s[p[i]], 此时 p[i+1] = p[i]+1

vector<int> prefix_function(string s) {
  int n = (int)s.length();
  vector<int> pi(n);
  for (int i = 1; i < n; i++)
    for (int j = pi[i - 1] + 1; j >= 0; j--)  // improved: j=i => j=pi[i-1]+1
      if (s.substr(0, j) == s.substr(i - j + 1, i+1)) {
        pi[i] = j;
        break;
      }
  return pi;
}

优化2

• 我们这个思路走得更远一点，讨论当 s[i+1] 不等于 s[p[i]] 时如何跳转。
• 失配时，我们希望找到对于子串 s[0 … i]，仅次于 p[i] 的第二长度 j，使得在位置 i 的前缀性质仍得以保持，也即：
• 如果我们找到了这样的长度 j，那么仅需要再次比较 s[i + 1] 和 s[j]。如果它们相等，那么就有 p[i + 1] = j + 1。否则，我们需要找到子串 s[0 … i] 仅次于 j 的第二长度 j^{(2)}，使得前缀性质得以保持，如此反复，直到 j = 0。如果 s[i + 1] 不等于 s[0]，则 p[i + 1] = 0。
• 我们可以得到一个关于 j 的状态转移方程：j^{(n)}=p[j^{(n-1)}-1]

vector<int> prefix_function(string s) {
  int n = (int)s.length();
  vector<int> pi(n);
  for (int i = 1; i < n; i++) {
    int j = pi[i - 1];
    while (j > 0 && s[i] != s[j]) j = pi[j - 1];
    if (s[i] == s[j]) j++;
    pi[i] = j;
  }
  return pi;
}

KMP

• 问题：给定一个文本 t 和一个字符串 s，我们尝试找到并展示 s 在 t 中的所有出现。
• 我们构造一个字符串 s + # + t，其中 # 为一个既不出现在 s 中也不出现在 t 中的分隔符。此时就能把问题转变成对新的字符串求前缀数组的新问题，由上述过程得知，用 O(n + m) 的时间以及 O(n) 的内存可解决该问题。

AC自动机

AC 自动机是 以 Trie 的结构为基础，结合 KMP 的思想 建立的自动机，用于解决多模式匹配。

其他

https://oi-wiki.org/string/